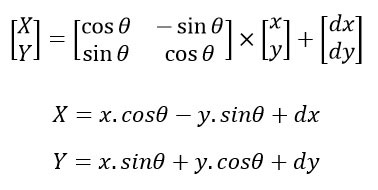همانطور که میدانید سیستم های مختصات، صرفنظر از اینکه در چه سیستم تصویری مورد استفاده قرار گیرند، وظیفه نمایش موقعیت عوارض در فضاهای یک بعدی، دو بعدی و بالاتر را دارند. مانند سیستم مختصات کارتزین، قطبی، استوانه ای و کروی که هرکدام با درنظرگرفتن مقادیر تعریف شده ای میتوانند موقعیت یک شیء را نمایش دهند. عمدتاً داده هایی که ما با آنها سروکار داریم در فضای دوبعدی تعریف شده و برای نمایش آنها از سیستم مختصات کارتزین استفاده میشود.
تبدیل سیستم مختصات در فضای کارتزین بسیار ساده است. کافیست فرمولی به شکل (X=F(x و (Y=G(y داشته باشیم تا بتوانیم مختصات نقاطی که در یک سیستم مختصات با x و y نمایش داده شده اند را به X و Y در سیستم مختصات دوم تبدیل کنیم. برای یک تبدیل ساده میتوانیم فرض کنیم که سیستم مختصات اولیه میتواند پس از اعمال دو جابجایی dx و dy و یک تغییر مقیاس S و یک دوران به اندازه θ بر سیستم مختصات دوم منطبق شود. در اینصورت با مشخص شدن چهار پارامتر میتوانیم تبدیل سیستم مختصات را انجام دهیم (تبدیل خطی). این معادلات بصورت زیر نوشته میشوند :
اما اگر فرض کنیم در یکی از سیستمهای مختصات، محورهای مختصات بر یکدیگر عمود نباشند و تغییر مقیاس در راستای X و Y یکسان نباشند، دو پارامتر دیگر نیز وارد میشوند و معادلات را به فرم زیر تغییر میدهند. دقت کنید که میتوانیم به جای استفاده از نسبتهای سینوسی و کسینوسی روابط بالا، از پارامترهای مجهول دیگری نیز استفاده کنیم.
باید در نظر داشته باشید که انتخاب معادلات مناسب برای تبدیل دو سیستم مختصات به نوع خطاهای موجود و پارامترهای تاثیرگذار آن وابسته است. یعنی اگر معادلاتی را انتخاب کنید که فرض آنها متعامد نبودن محورهای مختصات باشند، اما این خطا وجود نداشته باشد درواقع علاوه بر پیچیده تر کردن معادلات، میتوانید ایجاد خطا نیز بکنید. همچنین اگر تعداد مجهولات معادلات شما به اندازه پارامترهای تاثیرگذار نباشد، برخی از خطاها باقی خواهند ماند.
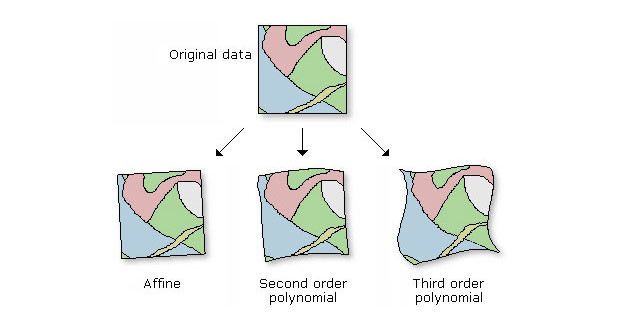
در عمل برای سهولت کار تبدیل سیستمهای مختصات در ژئورفرنس کردن، از درجات مختلف معادلات پلی نومیال (Polynomial) استفاده میکنند که فرمول آنها به قرار زیر است و در آنها معادلات درجات بالاتر، توانهای بالاتری از x و y را شامل میشوند.
درجه اول : X=ax+by+c و ‘Y=a’x+b’y+c
درجه دوم : X=ax2+by2+cx+dy+e و ‘Y=a’x2+b’y2+c’x+d’y+e
برای حل این معادلات از روش سرشکنی کمترین مربعات بهره برده میشود. حل این معادلات به تعداد مشاهدات وابسته است. مشاهدات در این مورد میتوانند ازطریق زوج مختصات هایی که در هر دو سیستم مختصات نمایش دهنده یک نقطه میباشند فراهم شوند. درواقع، معرفی هر نقطه مشترک بین دو سیستم تصویر، دو مشاهده و به تبع آن، دو معادله برای ما ایجاد میکند. تعداد مجهولات نیز باتوجه به مرتبه معادله تعیین میگردد. مثلاً برای معادله درجه اول تعداد مجهولات 6 تا است که مشابه حالت معادلات Affine میشود. درواقع معادلات پلی نومیال همان معادلاتی هستند که به بیان غیر مثلثاتی میتوانند پارامترهای دوران، جابجایی و غیره را مدل کنند.
با حل این معادلات پارامترهای مجهول به دست می آیند و سپس برای هر نقطه با مختصات x و y میتوانیم معادل X و Y آن را در سیستم مختصات ثانویه محاسبه کنیم. به این ترتیب تبدیل بین دو سیستم مختصات اتجام خواهد شد و برای تمامی نقاط از سیستم مختصات اولیه، نقاطی از سیستم مختصات ثانویه به دست خواهد آمد.
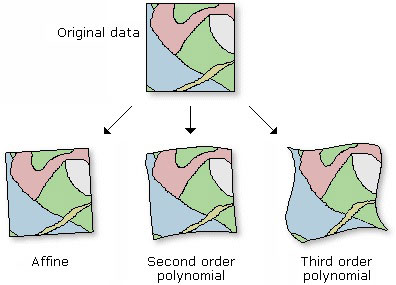
در نتیجه در ژئورفرنس کردن تصاویر، میبایست نقاطی را در معادله استفاده نمود که علاوه بر پوشش دادن کادر دور تصویر، داخل محدوده کار ما نیز دارای پخش مناسبی باشند و اصطلاحاً چگالی نقاط در بخشهای مختلف محدوده کار ما تقریباً یکسان باشد.